| B |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
Consider a collection of variables
{x1, x2, x3, ...}
that are distributed according to the function
Px(x),
then the probability of finding a value that lies between
x and
x+dx is
Px(x)dx.
If y is some function of
x then we can write:
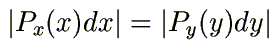
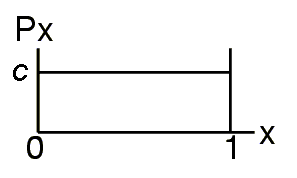 |
Px(x) = C (i.e. Uniform) and so Py(y) = C |dx/dy| |