B prev next
 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
<< MC APPLICATIONS >>

Random Walk

Assume that a walker is able to take steps length unity along a line as shown in Figure.

The walker begins at the origin (x=0) and each step is choosen at random to be either to the right or left each with probability 1/2.




PROBLEM:
Calculate 'Average Number of Steps' for the walker to be outside of the region [-a,+a].

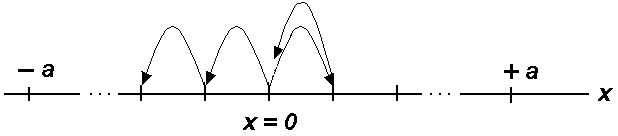
Algorithm: 

 Determine N  (Number of experiment)
 Determine a  (Border)
 Set sum = 0  (Sum of steps)

 LOOP1 from i=0 to N
     set step=0
     set x=0
     LOOP2 
          Generate a random number R 
          from a uniform distribution
          Take a step left or right:
          IF   R < 0.5 x=x-1 
          ELSE         x=x+1
          Increment step by 1

          Check IF |x| > a THEN 
            Add step to sum
            EXIT from LOOP2
          END IF
     END LOOP2
 END LOOP1 

 Set avrs = sum/N (Avr. Number of Steps)
 OUTPUT N, avrs

Output: For a = 3 

      N           avrs
-------------   ---------
           10   19.800000
          100   15.660000
        1,000   16.634000
       10,000   16.166200
      100,000   16.018900
    1,000,000   16.011948
   10,000,000   15.996875
  100,000,000   15.999419

The computer implementations of the algorithm : rw.f90 | rw.c