Electric Field Near a Straight Line Charge
and 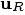 is the unit vector in the
direction of the vector
is the unit vector in the
direction of the vector 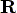 . Putting
. Putting
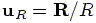 , Equation (1) becomes:
, Equation (1) becomes:
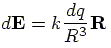 |
(3) |
By using vector a operation, the vector 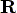 can be written in terms of position vector
can be written in terms of position vector
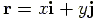 such that:
such that:
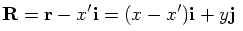 |
(4) |
and the length of 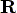 can be expressed as a
function of geometric parameters:
can be expressed as a
function of geometric parameters:
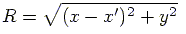 |
(5) |
The charge of the segment, 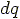 ,
can be written as:
,
can be written as:
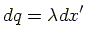 |
(6) |
Subsitution of Equations (4), (5) and (6) into Equation (3) yields:
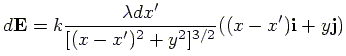 |
(7) |
The total electric field, 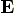 , is the
integral of electric field
, is the
integral of electric field 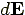 over the wire.
So, the componets of
over the wire.
So, the componets of 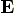 are found by evaluating the following integrals:
are found by evaluating the following integrals:
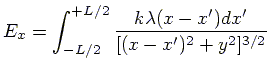 |
(8) |
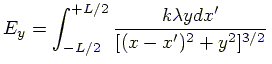 |
(9) |
In our program, we will evaluate these integrals numerially.
Integrating a function 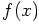 can be calculated by
Simpson's method.
The approximation to the integral is:
can be calculated by
Simpson's method.
The approximation to the integral is:
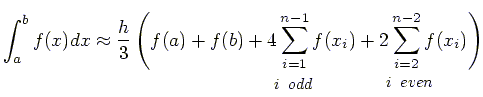 |
(10) |
where 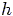 is a finite length of
is a finite length of
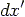 . Note that numerical errors can be
reduced by making
. Note that numerical errors can be
reduced by making 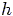 smaller.
The Simpson method in Equation (10) is used to solve the integrals
in Equation (8) and (9).
smaller.
The Simpson method in Equation (10) is used to solve the integrals
in Equation (8) and (9).
The computer programs in Fortran 90 and C can be found at:
linearCharge.f90 |
linearCharge.c
You can also download an executable visual program file produced by
Borland C++ Builder 1.0 from: linearCharge.exe
You can input 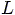 and
and
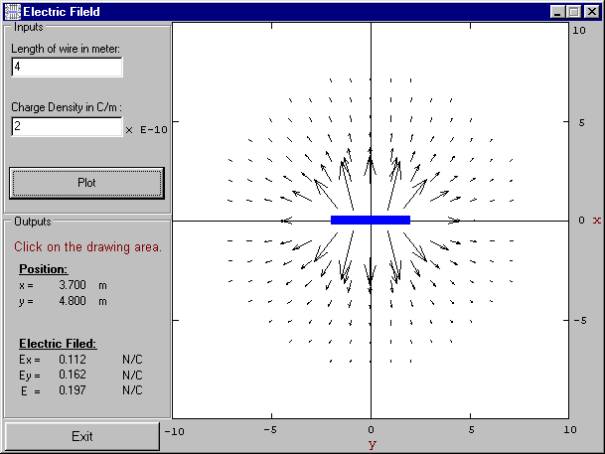
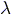 parameters and the program
plots the 2D-distribution of the electric field vectors,
parameters and the program
plots the 2D-distribution of the electric field vectors,
 .
.
Secreen Shots:
02_1.jpg |
02_2.jpg |
02_3.jpg
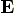 , at any point
, at any point
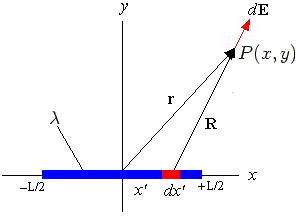
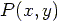 produced by a charged wire whose length is
produced by a charged wire whose length is
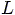 and has
a charge density (charge/length),
and has
a charge density (charge/length), 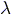 .
We assume that
the charge is spread uniformly along the wire, e.g.
.
We assume that
the charge is spread uniformly along the wire, e.g. 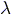 is a constant.
is a constant.
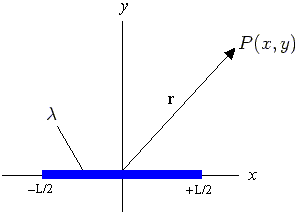
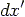 and carries the charge
and carries the charge
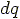 as shown in figure given left.
The electric field,
as shown in figure given left.
The electric field, 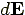 ,
produced by this segment, at a distance
,
produced by this segment, at a distance 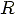 from it, is calculated from:
from it, is calculated from:
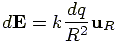
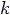 is a constant
and has the value:
is a constant
and has the value:
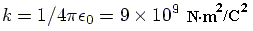
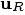 is the unit vector in the
direction of the vector
is the unit vector in the
direction of the vector 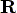 . Putting
. Putting
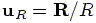 , Equation (1) becomes:
, Equation (1) becomes:
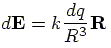
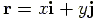 such that:
such that:
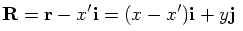
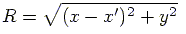
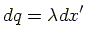
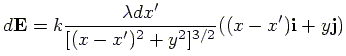
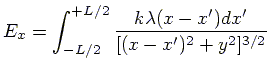
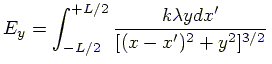
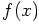 can be calculated by
can be calculated by
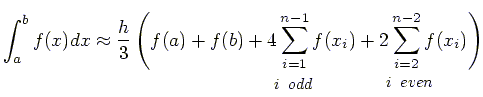
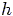 is a finite length of
is a finite length of
