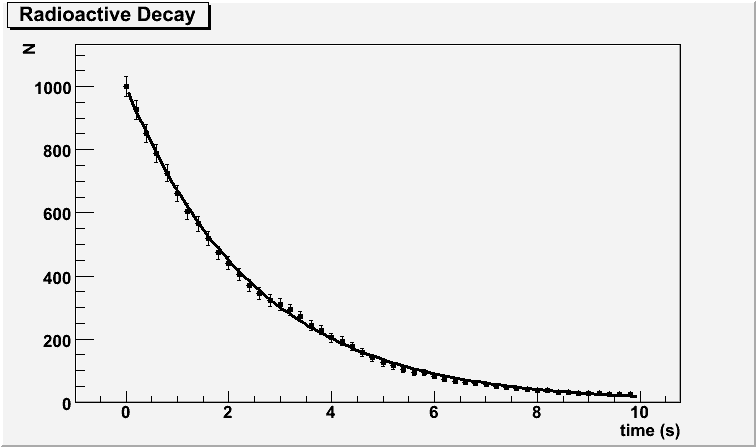
This is a truly random proceses. The probability of decay is constant. The probabilty that a nucleus undergoes radioactive decay in time dt is p:
p = λ dt (for λ dt <<1)
where λ (decay constant) is probability per unit time for the decay of each nucleus of a given nuclide.Consider a system initially having N0 unstable nuclei. How does the number of parent nuclei, N, change with time?
Theoretically, the number of undecayed nuclei at time t is given by:
N = N 0 exp (- λ t )
where N0 is the number of parent(undecayed) nuclei at t = 0.
Alogrithm:
Determine N0 (initial number of parents)
Determine λ (decay constant)
Determine Tmax (any time)
Determine dt (time step)
N = N0
LOOP from t=dt to Tmax, step dt
LOOP over each remaining parent nucleus
# Generate a random number R between [0,1] from a uniform distribution
R = uniform_RandomNumber()
# Decide if the nucleus decays:
# reduce the number of parents by 1
IF( R < λ dt ) N = N-1
END LOOP over nuclei
# calculate theoratical value
Ntheory = N0 * exp(-λt)
Record t, N and Ntheory
END LOOP over time
|
