Temel Yönleriyle Fortran 90 / 95 / 2003

  Temel Konular
* Önsöz

* Fortran'a Giriş
* Fortran'nın Temelleri
* Basit ve Formatlı Okuma/Yazma
* Temel Kütüphane Fonksiyonları
* Karşılaştırma Deyimleri
* Döngüler
* Alt Programlar I
* Alt Programlar II
* Diziler
* Dinamik Diziler
* Gösterici (Pointer) Kavramı
* Katarlar (Stringler)
* Yapısal Veri Tipleri
* Dosya Yönetimi
* Modül Kavramı
* Sayısal Tipler (KINDs)
* Bit Düzeyinde Çalışmak
* Kütüphane Fonksiyonları Listesi

* Yararlanılan Kaynaklar

  İleri Uygulamalar
* - - -
* Karmaşık Sayılar
* Tarih-Saat Fonksiyonları
* Rastgele Sayılar
* Katar - Sayı Dönüşümleri
* Komut Satırı İşlemleri
* Co-Array Fortran
* Derleme Seçenekleri
* Fortran ve C

  Seçilmiş Örnekler
* Sayılar Kuramı
* Analiz
* Lineer Cebir

  Fortran 90/95 Derleyicileri
* Salford (silversoft FTN95)
* G95
* GFORTRAN

  Dış Bağlantılar
* programlama.com
* Fortran (wikipedia)

* fortran.gantep.edu.tr
* g95.org
* Hot scripts

  İletişim
* E-posta

  

Bölüm 20: Karmaşık Sayılar

##################-- (%90)

Giriş

Karmaşık sayıların kullanımı daha çok mühendislik uygulamalarında karşımıza çıkar. Fortran Programlama dili kullanıcılarına Karmaşık sayılarla işlem yapmak için COMPLEX veri tipini sunarak büyük kolaylık sağlamıştır. Bu özellik bir çok programlama dilinde yoktur.

Hatırlarsak Bölüm 2'de, i2 = -1 olmak üzere, a + bi şeklindeki bir karmaşık sayı, Fortran'da 
      (a, b)
şeklinde ifade edildiği anlatılmıştı. Örneğin: 
     (3.0, 4.0)     ==>  3.0 + 4.0i
gibi.

20.1   Karmaşık (Complex) Sayı Fonksiyonları

Fortran 90+, karmaşık sayılar üzerinde işlem yapmak için aşağıdaki fonksiyonları kullanıcılarına sunmuştur:

  • AIMAG(Z)
    Z = x + iy karmaşık sayısının sanal (imaginary) kısmını gönderir.

  • REAL(Z)
    Z = x + iy karmaşık sayısının gerçel (real) kısmını gönderir.

  • CMPLX(X[,Y][,KIND])
    X + iY karmaşık sayını oluşturur.

  • CONJG(Z)
    Z = x + iy karmaşık sayısının eşleniği (complex conjugate) olan x - iy değerini gönderir.

  • ABS(Z)
    Z = x + iy karmaşık sayısının modülünü, sqrt(x**2 + y**2), gönderir.
Program 20.1'de bu fonksiyonların kullanımı gösterilmiştir.

Program 20.1: Sık kullanılan karmaşık sayı fonksiyonları 
01: 
02: 
03: 
04: 
05: 
06: 
07: 
08: 
09: 
10: 
11: 
12: 
13: 
14: 
15: 
16: 
17: 
18: 
19: 

PROGRAM Karmasik_Fonksiyonlar
!----------------------------------------------------
! 20prg01.f95
! Sık kullanılan karmaşık sayı fonksiyonları
!----------------------------------------------------
IMPLICIT NONE
COMPLEX :: Z

  Z = (3.0,  4.0) ! 3 + 4i

  PRINT *,"Z = ",Z
  PRINT *
  PRINT *,"AIMAG(z) = ",AIMAG(z)
  PRINT *," REAL(z) = ",REAL(z)
  PRINT *,"CONJG(z) = ",CONJG(z)
  PRINT *,"  ABS(z) = ",ABS(z)

END PROGRAM Karmasik_Fonksiyonlar

ÇIKTI 

 Z =  (3.,4.)

 AIMAG(z) =  4.
  REAL(z) =  3.
 CONJG(z) =  (3.,-4.)
   ABS(z) =  5.


20.2   Örnek Uygulamalar

ÖRNEK 1: EULER FORMÜLÜ

Kompleks Analizden bildiğimiz meşhur Euler Formülü:
şeklindedir. Fortran'da tanımlı REAL veri tipindeki fonksiyonlar aynı zamanda COMPLEX veri tipi için de çalışır. Buna dair bir örnek aşağıda verilmiştir.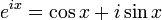

Program 20.2: Euler Formülü 
01: 
02: 
03: 
04: 
05: 
06: 
07: 
08: 
09: 
10: 
11: 
12: 
13: 
14: 
15: 

PROGRAM Euler_Acilimi
!----------------------------------------------------
! 20prg02.f95
! exp(ix) = cos(x) + i*sin(x) şeklide 
! yazılabileceğinin gösterimi.
!----------------------------------------------------
IMPLICIT NONE
COMPLEX :: i = (0.0,  1.0) !
REAL    :: x = 0.5         ! radyan

  PRINT *,"exp(i*x) = ",EXP(i*x)
  PRINT *,"cos(x)   = ",COS(x)
  PRINT *,"sin(x)   = ",SIN(x)

END PROGRAM

ÇIKTI 

 exp(i*x) =  (0.87758255,0.47942555)
 cos(x)   =  0.87758255
 sin(x)   =  0.47942555


ÖRNEK 2: KARMAŞIK KÖKLER

Program 5.4'de, ax2 + bx + c = 0 formundaki ikinci dereceden bir polinomun gerçel (reel) köklerini hesaplanmıştı. Daha genel bir çözüm karmaşık köklerin dahil edilmesidir. Program 20.3'de kuadratik denklemin gerçel köklerinin yanı sıra karmaşık kökerinini de bulur. Karmaşık köklerin bulunmasında CMPLX() fonksiyonu kullanılmıştır.

Program 20.3: Karmaşık Kökler 
01: 
02: 
03: 
04: 
05: 
06: 
07: 
08: 
09: 
10: 
11: 
12: 
13: 
14: 
15: 
16: 
17: 
18: 
19: 
20: 
21: 
22: 

PROGRAM Kuadratik
!-----------------------------------------------------------
! 20prg03.f95
! ax**2 + bx + c = 0 denkleminin gerçel ve karmaşık 
! (complex) köklerinin bulunması. Karmaşık köklerin
! bulunmasında CMPLX() fonksiyonu kullanılmıştır.
!-----------------------------------------------------------
IMPLICIT NONE
REAL :: a, b, c
COMPLEX :: Kok_Delta, x1, x2

    PRINT *, "a, b, c degerlerini girin:"
    READ *, A,B,C

    Kok_Delta = SQRT( CMPLX(B**2 - 4.0*A*C) )

    x1 = ( -B + Kok_Delta )/( 2.0*A )
    x2 = ( -B - Kok_Delta )/( 2.0*A )

    WRITE (*,*) "Kökler: ", x1, x2

END PROGRAM

ÇIKTI 

 a, b, c degerlerini girin:
1 1 1
 Kökler:  (-0.5,0.8660254) (-0.5,-0.8660254)

ÇIKTI 

 a, b, c degerlerini girin:
2 4 -8
 Kökler:  (1.236068,0.) (-3.236068,0.)


Powered by PHP