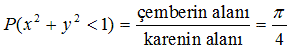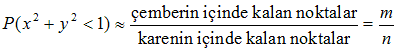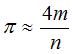C Programlama Dili'ne Giriş

  Dersler
* Önsöz

* Giriş
* Veri Tipleri, Değişkenler
* Operatörler
* Temel G/Ç Fonksiyonları
* Temel Kütüphane Fonksiyonları
* Karşılaştırma Deyimleri
* Döngüler
* Fonksiyonlar I
* Fonksiyonlar II
* Diziler
* Gösterici (Pointer) Kavramı
* Katarlar (Stringler)
* Dinamik Bellek Yönetimi
* Gösterici Uygulamaları
* Yapılar ve Birlikler
* Dosya Yönetimi
* Bit Düzeyinde Çalışmak
* Port Denetimi
* Grafik Kullanımı
* C Makroları

* Kısaca C++
* Derleme Seçenekleri
* Tarih-Saat Fonksiyonları
* Monte-Carlo Yöntemleri
* Fortran ve C

* Yararlanılan Kaynaklar

  C/C++ Derleyicileri
* Dev-C++
* Salford (silversoft FTN95)
* GCC
* Turbo C
* Eclipse IDE
* NetBeans IDE

  Dış Bağlantılar
* programlama.com
* C Programcıları Derneği

* C (wikipedia)
* C++ (wikipedia)
* cplusplus.com
* koders.com
* Hot scripts

  

Ders 24: Monte Carlo Yöntemleri

###################- (%95)

En son güncelleme: Wed, 30 Nov 2011 13:22:02 +0200
Giriş

Bilimsel uygulamalarda problemler iki kısımda incelenebilir:

  • kesin = deterministik (deterministic)
  • tahmini = olası (random).

Kesin sistemler, kuralları kanun hükmünde olan matematiksel yasalarla tanımlanabilen sistemlerdir; Örneğin yerçekimi yasası gibi. Burada başlangıç koşulları bilindiğinde sonucun ne olacağı kestirilebilir. Fakat, tahmini sistemlerin kuralları muhtemel veya raslantısal (stocastic) olan istatiksel yöntemlerle belirlenir; Örneğin havaya atılan bir metal paranın, yer düştüğünde yazı veya tura gelmesi gibi. Burada raslantıdan kasıt, tahmini sistemlerde, başlangıç koşulları kesin olarak tayin edilse bile, sonuca dair çözümün kesin olarak bilinememesi, ancak tahmin edilmesi anlamındadır. Yoksa, evrende raslantıya yer yoktur.

Bilgisayar ortamında, yazılımsal (veya donanımsal) olarak rastgele sayılar (random numbers) üretmek mümkündür. Monte Carlo Yöntemleri, bu rastgele sayıları kullanarak tahmini sistemleri modelleyen algoritmalardır. Aslında, Monte Carlo, (Fransa) Monako'nun kumarhaneleriyle ünlü en zengin yerleşim yeridir. (bkz. Wikipedia: Monte Carlo). Bu yüzden, tahmini sistemlerin modellenmeside kullanılan sayısal analiz yöntemlerine Monte Carlo (kısaca MC) ismi verilmiştir.

Bu bölümde, yazılımsal olarak üretilen Rastgele Sayılar ve Sayısal Analiz'de kullanılan basit Monte Carlo Yöntemleri konu edilecektir.


24.1   Uygulama Alanları

Monte Carlo (MC), rastgele sayıları baz alarak tahmini sistemleri modeller. Hatta, bazı kesin sistemlerde de kullanılabilir; Örneğin rastgele sayılarla Pi sayısını veya bir fonksiyonun integralini hesaplamak gibi. MC yöntemleri, Fizik ve Mühendislik alanlarında pekçok uygulama alanı bulmuştur. Bunlardan başlıcaları:

  • [Matematik] Sayısal Analiz
  • [Fizik] Doğal olayların simülasyonu
  • [Fizik] Atom ve Molekül Fiziği, Nükleer Fizik ve özellikle Yüksek Enerji Fiziği modellerini test eden simülasyonlar
  • [Mühendislik] Deneysel aletlerin (örneğin detektör) simülasyonu
  • [Biyoloji] Hücre Similasyonu
  • [Ekonomi] Borsa Modelleri
  • [İstatistik] Dağılım Fonksiyonları
Tahmini sistemleri modelleyebilmek için:
  • Rastgele Sayı üretmeyi ve kullanmayı
  • Basit MC programlarını oluşturmayı
  • İleri düzeyde hazırlanan MC üreteçlerini ve programları kullanmayı
iyi öğrenmek gerekir.

24.2   Rastgele Sayılar

Bilgisayarların en çok uygulandığı alanlardan bir tanesi kuşkusuz doğa olaylarının modellenmesidir. Bazı durumlarda, bilgisayarın ürettiği rastgele sayılar kullanılarak belirsiz yani tahmini sistemler modellenebilir. Rastgele sayı özel bir dağılımdan seçilen kargaşık (caotic) bir sayıdır.

Bilgisayarlar kesin (deterministic) bir yapıda çalıştıkları için gerçek anlamda rastgele sayı üretemezler. Ancak, uygun algoritmlarla bir bilgisayarın düzgün bir dağılımdan seçilen ve genllikle [0,1] arasında gerçel değerler alan rastgele sayı üretmesi sağlanabilir. Bilgisayarların ürettiği bu rastgele sayılar yalancı rastgele sayı (pseudo-random numbers) olarak adlandırılır. Rastgele sayı üreten bu algoritmalara rastgele sayı üreteci (random number generator) denir. Günümüz derleyicilerinin bir çoğunda rastgele sayı üreteçleri için hazır kütüphane fonksiyonları tanımlanmıştır.

Bu fonksiyonlar genellikle doğrusal bir denklem kullanarak, rastgele sayı dizisi üretir. 32-bit makinalarda, dizinin peryodu en az 231 ~ 109 (1 milyar) dur. Yani, bir rastgele sayı üreteci birbirinden farklı 1 milyar farklı sayı üretebilir. Bu kadar çok sayı günümüz bilgisaylarında bir kaç saniyede kolaylıkla oluşturulabilir.

Rastgele sayı dizisini oluşturacak doğrusal denklemin genel biçimi şöyledir:
xn+1 = ( a xn + b ) mod m

burada mod modüler aritmetik işlemi anlamındadır. Dizinin ilk elemanı, xo, çekirdek (seed) olarak adlandırılır. a ve b sabitleri, dizi elemanları kargaşık ve düzgün dağılacak şekilde seçilir.

1960 yılında IBM şirketi aşağıdaki meşhur RANDU algoritmasını kullanmıştır (a = 69069, b = 0):
xn+1 = ( 69069 xn ) mod 231-1
Daha sonra Park ve Miller, aşağıdaki Minimal Standart algoritmasını önermiştir (a = 16807, b = 0):
xn+1 = ( 16807 xn ) mod 231-1
Park-Miller algoritması ile oluşturulan rastgele sayı üreteci, aşağıdaki C fonksiyonu ile kotarılabilir: 
     /*
      * Park-Miller algoritması ile [0,1] arasında
      * düzgün dağılmış rastgele sayı üretir. 
      */
     float rastgele(int *cekirdek)
     {
        const int  im = 2147483647, ia = 16807;
        const int  iq = 127773,     ir = 2836;
        const float m = 128.0/im;
        int   k;
        float r;

        k = *cekirdek / iq;
        *cekirdek = ia*(*cekirdek-k*iq) - ir*k;

        if(*cekirdek < 0) *cekirdek += im;

        r = m * (*cekirdek/128);

        return r;
     }

Program 24.1'de, rastgele() fonksiyonu kullanılarak 10 sayı üretilmiştir. Program her çalıştırıldığında aynı sayılar üretilecektir. Bunun nedeni kümenin ilk elemanı ilk_sayi sabit olmasıdır.

Program 24.1: 10 rastgele sayı 
01: 
02: 
03: 
04: 
05: 
06: 
07: 
08: 
09: 
10: 
11: 
12: 
13: 
14: 
15: 
16: 
17: 
18: 
19: 
20: 
21: 
22: 
23: 
24: 
25: 
26: 
27: 
28: 
29: 
30: 
31: 
32: 
33: 
34: 
35: 
36: 
37: 
38: 
39: 
40: 
41: 
42: 
43: 
44: 
45: 
46: 

/* 24prg01.c
   rastgele() fonksiyonu ile 10 adet [0-1] arasında 
   rastgel sayı üretir */

#include <stdio.h>

float rastgele(int *);

int main()
{
  int ilk_sayi, i;
  float r;

  /* dizinin çekirdeği (seed) */
  ilk_sayi = 123456789;

  for(i=1; i<=10; i++){
    r = rastgele( &ilk_sayi );
    printf("%f\n",r);
  }

  return 0;
}

/*
 * Park-Miller algoritması ile [0,1] arasında
 * düzgün dağılmış rastgele sayı üretir. 
 */
float rastgele(int *cekirdek)
{
     const int  im = 2147483647, ia = 16807;
     const int  iq = 127773,     ir = 2836;
     const float m = 128.0/im;
     int   k;
     float r;

     k = *cekirdek / iq;
     *cekirdek = ia*(*cekirdek-k*iq) - ir*k;

     if(*cekirdek < 0) *cekirdek += im;

     r = m * (*cekirdek/128);

     return r;
}

ÇIKTI 

0.218418
0.956318
0.829509
0.561695
0.415307
0.066119
0.257578
0.109957
0.043829
0.633966


24.3   ANSI C Fonksiyonları

Standart C (ve C++), RANDU ve Minimal Standart'a göre daha verimli çalışan (stdlib.h başlık dosyasında bildirilen) aşağıdaki iki fonksiyonu kullanıcılarına sunmuştur:

  • int rand(void)
    0 ile RAND_MAX arasında tamsayı tipinde yalancı rastgele sayı üretilir.
    RAND_MAX, stdlib.h'de tanımlı sembolik bir sabittir. Değeri (derleyiciye bağlı olarak) en büyük int limiti ile sınırlıdır. Bu değer Turbo C (16-bit) derleyicisinde: 
          #define RAND_MAX  32767
    şeklinde, gcc gibi (32-bit) uygulamalarda: 
          #define RAND_MAX  2147483647
    şeklinde tanımlanmıştır.

  • void srand(unsigned int cekirdek)
    Rastgele sayı üreteci (rand()) için cekirdek değerini belirler.
Aşağıda bu fonksiyonların uygulamaları gösterilmiştir. İnceleyiniz.

Program 24.2: 
01: 
02: 
03: 
04: 
05: 
06: 
07: 
08: 
09: 
10: 
11: 
12: 
13: 
14: 
15: 
16: 
17: 
18: 

/* 24prg02.c
   rand() ile 10 adet rastgele tamsayı sayı üretir */

#include <stdio.h>
#include <stdlib.h>

int main()
{
   int i;

   /* rand fonksiyonu */
   for(i=1; i<=10; i++)
     printf("%d\n",rand());

   printf("RAND_MAX = %d\n",RAND_MAX);

 return 0;
}

ÇIKTI 

1804289383
846930886
1681692777
1714636915
1957747793
424238335
719885386
1649760492
596516649
1189641421
RAND_MAX = 2147483647


Program 24.3: 
01: 
02: 
03: 
04: 
05: 
06: 
07: 
08: 
09: 
10: 
11: 
12: 
13: 
14: 
15: 
16: 
17: 
18: 

/* 24prg03.c
   rand() ile 10 adet [0,1] arasında rastgele gercel sayı üretir */

#include <stdio.h>
#include <stdlib.h>

int main()
{
   int i;

   /* rand fonksiyonu */
   for(i=1; i<=10; i++)
     printf("%f\n",(float) rand()/RAND_MAX);

   printf("RAND_MAX = %d\n",RAND_MAX);

 return 0;
}

ÇIKTI 

0.840188
0.394383
0.783099
0.798440
0.911647
0.197551
0.335223
0.768230
0.277775
0.553970
RAND_MAX = 2147483647


Program 24.4: 
01: 
02: 
03: 
04: 
05: 
06: 
07: 
08: 
09: 
10: 
11: 
12: 
13: 
14: 
15: 
16: 
17: 
18: 
19: 
20: 

/* 24prg04.c
   rand() ile 10 adet rastgele gercel sayı üretir */

#include <stdio.h>
#include <stdlib.h>

int main()
{
   int i, cekirdek;

   /* cekirdeği değiştir */
   cekirdek = 31415926;
   srand(cekirdek);

   /* rand fonksiyonu */
   for(i=1; i<=10; i++)
     printf("%f\n", (float) rand()/RAND_MAX);

 return 0;
}

ÇIKTI 

0.474201
0.796722
0.873683
0.191069
0.541366
0.672161
0.454705
0.901691
0.926034
0.197616


Program 24.5: 
01: 
02: 
03: 
04: 
05: 
06: 
07: 
08: 
09: 
10: 
11: 
12: 
13: 
14: 
15: 
16: 
17: 
18: 
19: 
20: 
21: 
22: 

/* 24prg05.c
   rand() ile 10 adet rastgele gercel sayı üretir */

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

int main()
{
   int i, cekirdek;

   /* cekirdeği time fonksiyonundan seç.
      Bu sayede program her çalıştığında farklı küme üretir. */
   cekirdek = time(NULL);
   srand(cekirdek);

   /* rand fonksiyonu */
   for(i=1; i<=10; i++)
     printf("%f\n", (float) rand()/RAND_MAX);

 return 0;
}

ÇIKTI 

0.789827
0.934420
0.980876
0.453894
0.115219
0.993930
0.945253
0.023599
0.851912
0.334151



24.4   Basit Monte Carlo Programları

Bu kısımda, rastgele sayılar kullanılarak üç basit MC uygulaması verilmiştir.


Uygulama 1: Yazı-Tura Simülasyonu

Hilesiz bir para atıldığında, yazı veya tura gelme olasılığı (P, probability) eşit ve kuramsal olarak P = 1/2 dir. Düşünün ki bir para n kez atılsın ve gelen turaları sayalım ve t ile gösterelim. Deney sayısı, n, arttıkça t/n oranı kararlı (sabit) kalmaya başlar. Bu durumda, olasılığın istatiksel tanımı şöyle yapılır:

P(t) = t/n
n sonsuza giderken P(t) değeri P = 1/2 değerine yaklaşır.

Şimdi, [0, 1] aralığından rastgele seçilen sayıları kullanarak, para atma deneyini yapalım. Rastgele sayı üreteçleri sayıları eşit olasılıkla üretir. r bir rastgele sayı olsun. r < 0.5 durumuna tura, r >= 0.5 durumuna da yazı diyelim. Bu şekilde, bir döngü kullanarak deney sayısına (n) göre, yazı-tura simulasyonu yapılabilir. Program 24.6, klavyeden girilen n'ye göre, P(t) ve 1 - P(t) olasılıklarını hesaplar.

Program 24.6: Yazı-Tura Simulasyonu 
01: 
02: 
03: 
04: 
05: 
06: 
07: 
08: 
09: 
10: 
11: 
12: 
13: 
14: 
15: 
16: 
17: 
18: 
19: 
20: 
21: 
22: 
23: 
24: 
25: 
26: 
27: 
28: 
29: 
30: 
31: 
32: 
33: 
34: 
35: 
36: 
37: 
38: 
39: 
40: 
41: 

/* 24prg06.c
   MC Yazı-Tura Simulasyonu */

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

/* [0, 1] arası rastgele sayı gönderir */
double rastgele(){
  double r = (double) rand()/RAND_MAX;
  return r;
}

int main()
{
   int i, tura, yazi, n;
   double r, p;

   /* deney sayısı */
   printf("deney sayisini girin: ");
   scanf("%d",&n);

   /* rastgele sayı üretecini başlat */
   srand( time(NULL) );   

   /* deneyleri başlat */
   for(tura=0, i=1; i<=n; i++){
     r = rastgele();
     if(r<0.5) tura++;
   }

   p = (double) tura/n;
   yazi = n-tura;

   /* sonuçlar ekrana */
   printf("tura sayisi: %d\n",tura);
   printf("yazi sayisi: %d\n",yazi);
   printf("Olasiliklar: %lf  %lf\n",p, 1.0-p);

 return 0;
}

ÇIKTI 

deney sayisini girin: 150
tura sayisi: 76
yazi sayisi: 74
Olasiliklar: 0.506667  0.493333


Program 24.7'de deney sayısı (n) bir dış döngüye bağlanarak, 10'un katları (10, 100, 1000, ...) olarak değiştirilmiştir. Programın çıktısı sırasıyla, n, gelen tura sayısı, gelen yazı sayısı ve tura ve yazı olasılıklarıdır. n büyüdükçe, p'nin 0.5'e yaklaştığına dikkat edin.

Program 24.7: Yazı-Tura Simulasyonu 
01: 
02: 
03: 
04: 
05: 
06: 
07: 
08: 
09: 
10: 
11: 
12: 
13: 
14: 
15: 
16: 
17: 
18: 
19: 
20: 
21: 
22: 
23: 
24: 
25: 
26: 
27: 
28: 
29: 
30: 
31: 
32: 
33: 
34: 
35: 
36: 
37: 
38: 
39: 
40: 
41: 
42: 

/* 24prg07.c
   MC Yazı-Tura Simulasyonu */

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>

/* [0, 1] arası rastgele sayı gönderir */
double rastgele(){
  double r = (double) rand()/RAND_MAX;
  return r;
}

int main()
{
   int    i, j, tura, yazi, n;
   double r, p;

   /* rastgele sayı üretecini başlat */
   srand( time(NULL) );   

   for(j=1; j<=8; j++){

      /* deney sayısı 10'un katları */
      n = pow(10, j);

      /* deneyleri başlat */
      for(tura=0, i=1; i<=n; i++){
         r = rastgele();
         if(r<0.5) tura++;
      }

      p = (double) tura/n;
      yazi = n-tura;

      /* sonuçlar ekrana */
      printf("%9d : %9d %9d  | %10.7lf %10.7lf\n",n, tura, yazi, p, 1.0-p);
   }

 return 0;
}

ÇIKTI 

       10 :         7         3  |  0.7000000  0.3000000
      100 :        39        61  |  0.3900000  0.6100000
     1000 :       530       470  |  0.5300000  0.4700000
    10000 :      5006      4994  |  0.5006000  0.4994000
   100000 :     50116     49884  |  0.5011600  0.4988400
  1000000 :    500200    499800  |  0.5002000  0.4998000
 10000000 :   5002805   4997195  |  0.5002805  0.4997195
100000000 :  49996285  50003715  |  0.4999629  0.5000372



Uygulama 2: Zar Simülasyonu

Bu uygulamada, bir çift zar atımı modellenecektir. Bu, bir çok tavla programında kullanılan yöntemdir. Bir çift zar atılıyor. Zarların toplamının 7 olma olasılığını bulan bir program yazalım (Program 24.8). Zar, [1, 6] arasında rastgele tamsayı değeri alır. Buna göre, r [0,1] arasında rastele gerçel sayı ise, bir zarın MC modeli: zar = 1 + tamsayı(6*r) şeklinde olur. Neden?

Program 24.8: Zar Simulasyonu 
01: 
02: 
03: 
04: 
05: 
06: 
07: 
08: 
09: 
10: 
11: 
12: 
13: 
14: 
15: 
16: 
17: 
18: 
19: 
20: 
21: 
22: 
23: 
24: 
25: 
26: 
27: 
28: 
29: 
30: 
31: 
32: 
33: 
34: 
35: 
36: 
37: 
38: 
39: 
40: 
41: 
42: 
43: 
44: 
45: 
46: 
47: 
48: 
49: 
50: 
51: 
52: 
53: 
54: 

/* 24prg08.c: MC Zar Simulasyonu 
   Atılan bir çift zarın toplamının yedi olma olasılığını hesaplar.

   Olasılık kuramına göre, birçift zarın toplamının 7 olma olasılığı 
   aşağıdaki formülden hesaplanabilir:
     Ptoplam(7) = P(1,6) + P(2,5) + P(3,4) + P(4,3) + P(5,2) + P(6,1)

   Diğer taraftan:
     P(1,6) = P(2,5) = P(3,4) = P(4,3) = P(5,2) = P(6,1) = 1/36'dır.

   Buna göre:
     Ptoplam(7) = 6*(1/36) = 1/6 = 0.16666.. dır. */

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>

/* [0, 1] arası rastgele sayı gönderir */
double rastgele(){
  double r = (double) rand()/RAND_MAX;
  return r;
}

int main()
{
   int    i, j, n, zar1, zar2, yedi;
   double p;

   /* rastgele sayı üretecini başlat */
   srand( time(NULL) );   

   for(j=1; j<=8; j++){

      /* deney sayısı 10'un katları */
      n = pow(10, j);

      /* deneyleri başlat */
      for(yedi=0, i=1; i<=n; i++)
      {
         /* iki adet rastgele sayı */
         zar1 = 1 + (int) 6.0*rastgele();
         zar2 = 1 + (int) 6.0*rastgele();
         if( (zar1+zar2) == 7 ) yedi++;
      }

      p = (double) yedi/n;

      /* sonuçlar ekrana */
      printf("%9d : %9d  |  %10.7lf\n",n, yedi, p);
   }

 return 0;
}

ÇIKTI 

       10 :         1  |   0.1000000
      100 :        20  |   0.2000000
     1000 :       151  |   0.1510000
    10000 :      1617  |   0.1617000
   100000 :     16730  |   0.1673000
  1000000 :    166931  |   0.1669310
 10000000 :   1666210  |   0.1666210
100000000 :  16663659  |   0.1666366



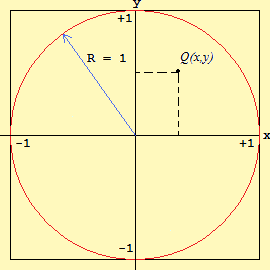
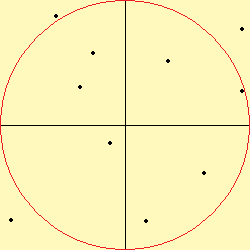
Uygulama 3: MC ile Pi sayısının hesabı
Yanda verilen şekildeki gibi bir karenin içine teğet olarak yerleştirilmiş bir çember düşünelim. Karenin bir kenarı 2 birim veya çemberin yarıçapı R = 1 birim olsun (birim çember). Karenin içinde, koordinatları (x, y) olan rastgele bir Q noktası seçilsin. Q noktasının koordinatları x2 + y2 < 1 şeklinde seçilmişse, Q noktası çemberin içinde, aksi halde nokta çemberin dısşında demektir. Bu kurumda, Q noktasının çemberin içinde kalma ihtimali şöyle olur:

Karenin içi n adet rastgele noktalarla doldurulsun. Eğer bu n noktanın, m tanesi çemberin içinde kalırsa, herhangi bir noktanın çemberin içinde kalma ihtimali yaklaşık olarak:

şeklinde olur. Bu iki denklem birleştirilirse, pi sayısı (yaklaşık olarak)

şeklinde hesaplanabilir.

Olayın canlandırılması adına, aşağıda nokta sayısının (n) farklı değerleri için oluşabilecek desenler gösterilmiştir.

n = 10 nokta n = 100 nokta n = 200 nokta


Program 24.9'da, MC yöntemi ile pi sayısının hesabı gösterilmiştir. Program ayrıca, hesaplanan pi ile math.h'de tanımlı sabit M_PI arasındaki hatanın yüzde olarak karşılığnı da ekranda gösterir. Program çıktısı incelendiğinde, hata n = 10 için yüzde 10, n = 1 milyar için yüzbinde 2 civarındadır.

Program 24.9: MC ile Pi sayısının hesabı 
01: 
02: 
03: 
04: 
05: 
06: 
07: 
08: 
09: 
10: 
11: 
12: 
13: 
14: 
15: 
16: 
17: 
18: 
19: 
20: 
21: 
22: 
23: 
24: 
25: 
26: 
27: 
28: 
29: 
30: 
31: 
32: 
33: 
34: 
35: 
36: 
37: 
38: 
39: 
40: 
41: 
42: 
43: 
44: 
45: 
46: 
47: 
48: 
49: 

/* 24prg09.c: 
   MC Yöntemi ile pi sayısının hesaplanması */

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>

/* [0, 1] arası rastgele sayı gönderir */
double rastgele(){
  double r = (double) rand()/RAND_MAX;
  return r;
}

int main()
{
   int    i, j, n, m;
   double x, y, pi, hata;

   /* rastgele sayı üretecini başlat */
   srand( time(NULL) );   

   for(j=1; j<=8; j++){

      /* deney sayısı 10'un katları */
      n = pow(10, j);

      /* deneyleri başlat */
      for(m=0, i=1; i<=n; i++)
      {
         /* [-1, 1] aralığında iki adet rastgele sayı */
         x = -1 + 2.0*rastgele();
         y = -1 + 2.0*rastgele();
         if( x*x + y*y < 1.0 ) m++;
      }

      /* deney sonucu hesaplanan pi */
      pi = (double) 4.0*m/n;

      /* hesaplanan ve gerçek pi arasındaki yüzde mutlak hata */
      hata = 100.0*fabs(pi-M_PI)/M_PI;

      /* sonuçlar ekrana */
      printf("%9d : %9d  |  pi = %10.7lf  , yuzde hata = %%%10.7lf\n", 
              n, m, pi, hata);
   }

 return 0;
}

ÇIKTI 

        10 :          7  -->  pi =  2.8000000 , yuzde hata = %10.8732319
       100 :         78  -->  pi =  3.1200000 , yuzde hata = % 0.6873155
      1000 :        794  -->  pi =  3.1760000 , yuzde hata = % 1.0952199
     10000 :       7878  -->  pi =  3.1512000 , yuzde hata = % 0.3058113
    100000 :      78625  -->  pi =  3.1450000 , yuzde hata = % 0.1084592
   1000000 :     785728  -->  pi =  3.1429120 , yuzde hata = % 0.0419961
  10000000 :    7853164  -->  pi =  3.1412656 , yuzde hata = % 0.0104104
 100000000 :   78536996  -->  pi =  3.1414798 , yuzde hata = % 0.0035910
1000000000 :  785380671  -->  pi =  3.1415227 , yuzde hata = % 0.0022272


Powered by PHP